Easter Maths Challenge

I tackled a decision problem using optimisation of routes between towns. I was unsatisfied with the answer and wrote a simulation (1200 lines of code) to find out. Our first guess was in fact the most efficient.

 

An up to date copy is running here.

Instructions for original challenge are here.

 

You can click through routes and it automatically does everything for you such as preparing the table, counting eggs etc… The main reason I made this was for the 'brute force' method to look good.

 

I then went and made a ‘random route’ generator that essentially just rolls a dice for each stage and decides where to go until it is below a certain value of carrots / miles in which it stops and returns the value. If it is above a threshold it would then allow me to view it. It is very quick but not great in terms of finding the best optimal solution if it is unknown as of course it could be just by chance that you miss the optimal route. I also used the same function to create a distribution table function that would return a spreadsheet with the egg counts tied to how many occurrences in a cycle of iterations. I left this running for around 10,000,000,000 iterations (of workers - simulations that try out a route). Even with how fast this function was in comparison to brute forcing it took around 2.5 days to finish. The results are shown below.

 

 

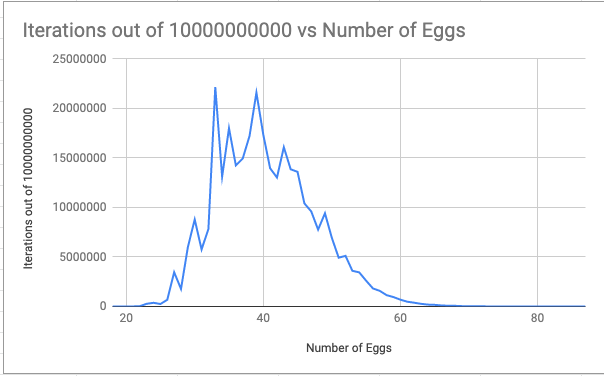
I also logged whenever the value was above 86 and downloaded the route, they are exactly the same as our route in the session (attached).

 

Although this was pretty reliable in indicating that 87 was probably the tail end, I was not using some kind of algorithm to prove that this is the case. I enlisted some assistance from a friend who is an expert at this technique called Dynamic Programming which is basically using what you already know to solve a problem more efficiently. Brute force would have a Big O (essentially how time consuming it would be) of n! In this case n being 24 so 6.2x10^23. Not ideal. This dynamic programming technique uses a technique shown below to get it down to a Big O of O(2^n n^2) which is still quite bad but a lot more realistic than n! This would be 9,663,676,416 for this problem.

 

This image is from: https://medium.com/basecs/speeding-up-the-traveling-salesman-using-dynamic-programming-b76d7552e8dd which is a nice way of explaining it.

 

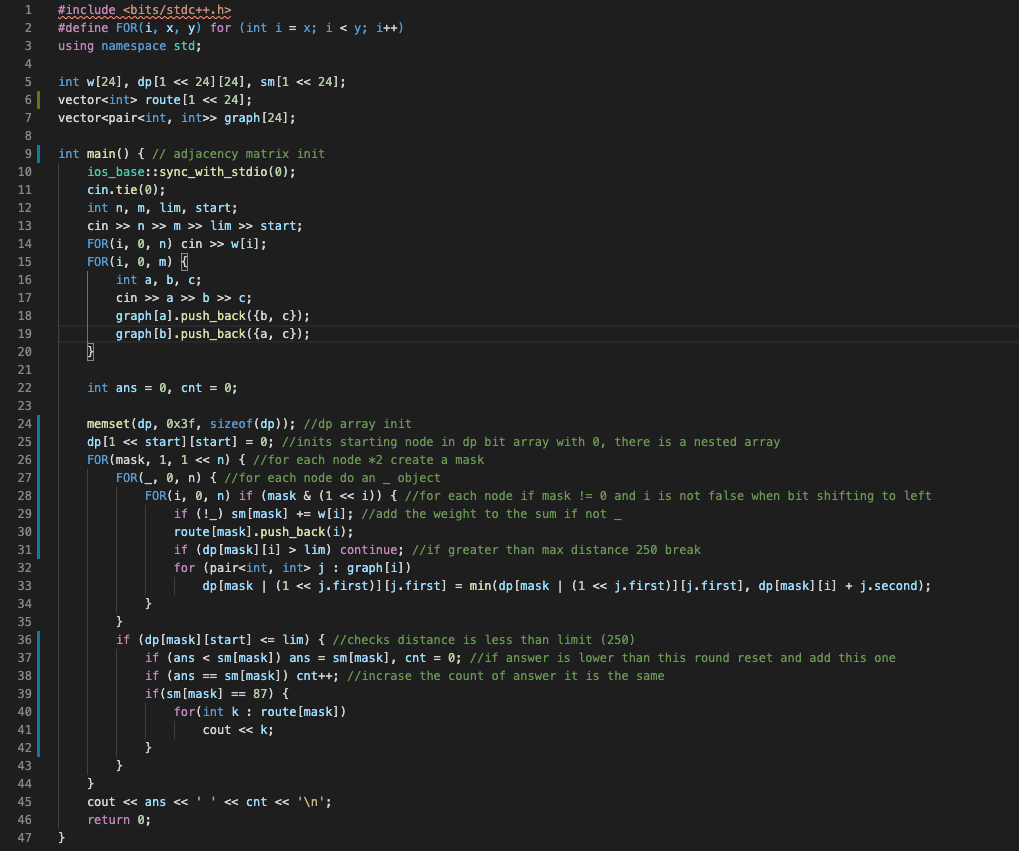
So he managed to work his magic using bitwise operations (essentially having a binary string of characters for each town and switching them to 1 or 0 depending on whether they were visited) to very quickly work out the maximum number of eggs possible for this graph. This was originally in a medium level language, C++ but in order to get it to work with the simulator I needed to convert it to something called JavaScript which is not as performant.

 

However as amazing as it is, there are some limitations such as the fact that it must store all the bit masks until it is complete which uses quite a bit of memory as you can imagine. This also means that as it is working on all of them as it goes along, it cannot keep track of the route. I tried to implement the logic in order for this to happen but it crashed within 10 seconds with an out of memory error…

 

C++ Code from a friend - my comments were me trying to decipher what was going on:

 

My conversion:

 

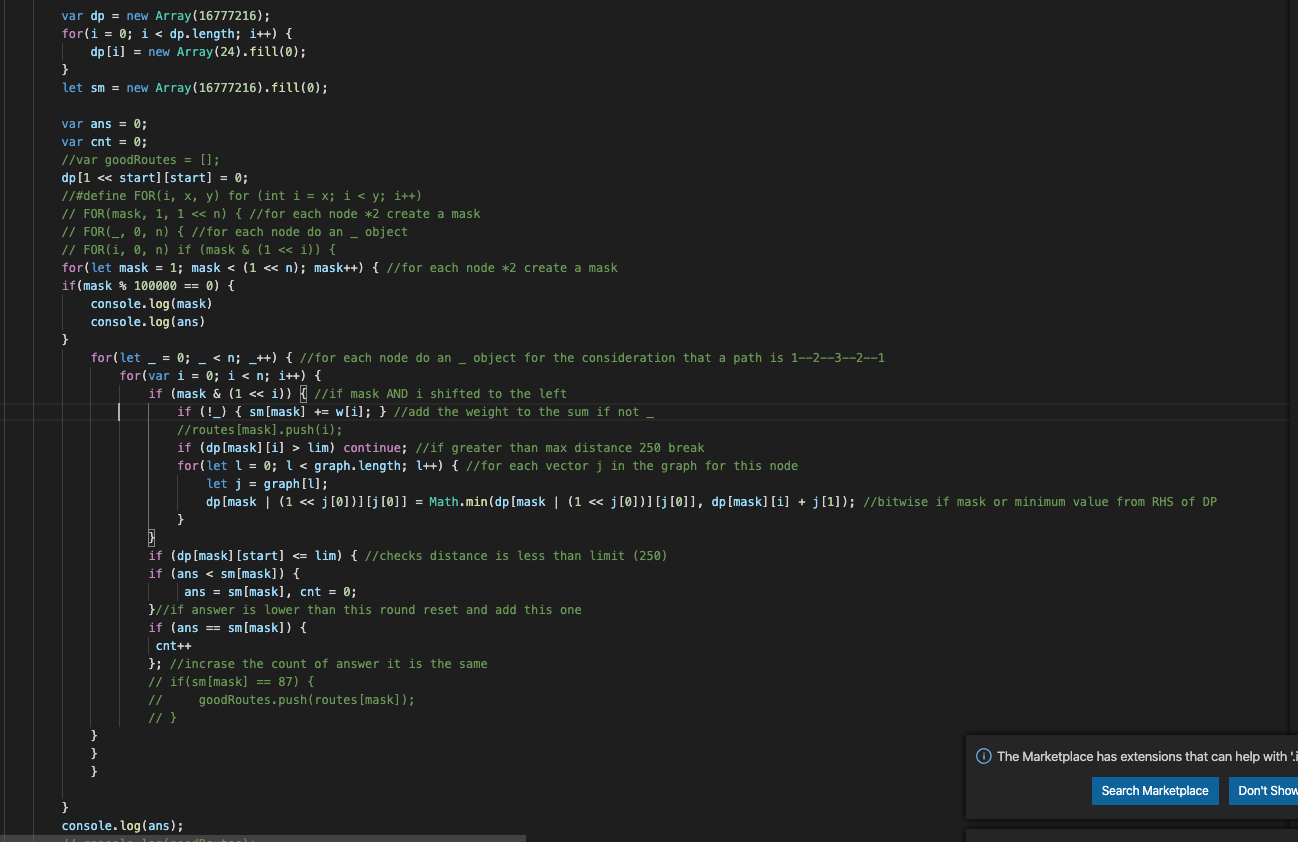
Unfortunately I broke my JS version when trying to get it to store the route. But the C++ version came out with the outcome that 2 sets of nodes supposedly have an egg count of 87 (which was the max value). This lines up with the distribution table from above so I am taking this as the final answer.